Tree Learner

A prominent as well as simple concept in supervised learning are decision trees. Firstly mentioned in the mid ’20 century in research, the concept gained remarkable popularity due to its simplicity and the great possibility of interpretation of the results.

In general, a decision tree is a function with a tree-like structure of decision rules. The tree is induced based on the underlying training data and outputs a prediction for the target variable when it is confronted with (unseen) input data.

The present article provides a solid explanation of the underlying concept, the specifications and the application of decision trees.

The Algorithm

As every concept in supervised learning, the goal of a decision tree is to predict a target variable based on unseen input data after having trained a model with data from the same data source. Therefore an algorithm, also called inducer, automatically learns the structure of the underlying (training) data top-down. It constructs a decision tree using specific decision rules to split the data in more and more homogenous partitions at each level of the tree down to the leaves.

Within the prediction phase the constructed model can then be used to apply the established decision structure on the unseen data from the stump down to the leaves.  The final prediction for an input sample is built in the leaves.

In Table 1, a dataset with the input data X^{nxp} (the attributes of a respective animal) and the target variable Y \, \epsilon \, \{cat,dog\} is shown.

Table 1: Introductory example data

In order to predict the unknown target variable of unseen input data, a tree can be built upon the training data. The chosen inducer proceeds mainly as follows:

At the so-called root node, the feature to split the data on has to be found to break the data down in the most homogenous partitions. For example, as shown in Figure 1, the feature height is the optimal feature to split on at the root node, resulting in three new decision nodes containing respectively all animals being small, medium big and tall.

In the resulting decision nodes, the best feature to break the data further down in more homogenous partitions has to be found. For example, the small animals on the left of the decision tree in Figure 1 can be split up with regard to the weight, resulting in the three leaves or  terminal nodes of the tree. The same procedure is applied on the other branches of the tree until for each branch the leaves are reached or a predefined stopping criterion is met.

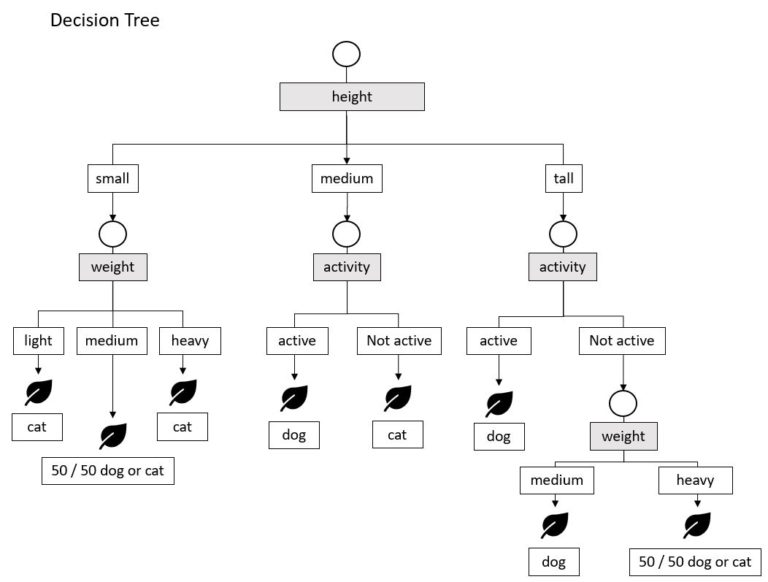
Figure 1: Examplary grown decision tree on data of table 1

The fashion, the inducer proceeds can be called a “greedy Divide & Conquer” approach, because the tree tries to split the data at each node using the most optimal feature in terms of data purity. The resulting tree tends to become, depending on the underlying data, very complex causing the tree to overfit. Therefore popular inducer such as C4.5, C5.0 or CART provide stopping criterion and/or implementation of pruning methods where the integral tree is trimmed down to the most optimal structure. In this way, a tree can be obtained that offer a good generalization and does not overfit the training data.
Getting back to the present example, after having created the tree, it can be used with unseen input data to predict Y with the estimation \hat{Y} . In Figure 2, an example for the prediction of unseen data from the data source in Table 1 is exposed.

Figure 2: Path of a sample through the decision tree established in figure 1

In general, splits with less outgoing branches are preferred over multiway splits, because multiway splits fragment the data too quickly. When the data is too fragmented in nodes further down the tree, the data left can be insufficient to make good predictions. But the number of outgoing branches depends strongly on the chosen inducer.

Having now a solid understanding of the general functioning, the question arises why the greedy approach in an iterative fashion is used to find a solution for the optimal tree structure:

Imagining a random data set with n features X which can be either true or false. A function maps the two input features onto a dependent feature Y. If both features are true, Y is also true. Otherwise Y is false.

The truth table resumes the possible combinations of the input variables. Writing down the truth table over the n features results in a matrix with   2^2 rows (e.g. Table 2) what can be understood as the number of nodes in the possible decision trees. 

Table 2: Truth Table for 2 attributes

But these nodes in turn can be arranged in multiple ways, resulting in multiple possible decision trees. For binary features e.g. exist for each node 2 possibilities to choose from. So, there possibly exist 2^n (here: 2^2) functions and even more trees because more than one tree can describe the same function.

For a problem with ten features, there are at least 2^{(2^{10})}=2^{1024}=1,79 x 10^{308}  possible trees to go through, what could even for a highly performant system a time consuming if not infeasible task.

Consequently, it is necessary to approach such problems in a more heuristic manner. The greedy “Divide & Conquer” approach is used as a heuristic in popular decision tree inducer.

The Algorithm

There are different tree inducers to grow decision trees. But in general, they follow the same framework. In Algorithm 1, this framework is shown to shed a bit light on the concept.

Algorithm 1: General framework of tree inducer

Impurity-based Criteria

Considering a random variable X which takes k discrete, categorical values which are distributed according to P=( p_{1} , p_{2},…, p_{k}).
The function \Phi is impurity measure that describes the disorder within a given data set. The following characteristics are typical for \Phi:

    • it is always above zero: \Phi(P) \geq 0
    • The function shows its minimum, if there exists one of k values i where p_{i}=1 and necessarily \forall j \neq i = 0
    • The function reaches its maximum, if \foralli, 1\leqi\leqk, p_{i}=\frac{1}{k}
    • \Phi(P) is symmetric
    • \Phi(P) is differentiable everywhere

if the random variable or the data set in question satisfies the second condition above, in other words if there is one i where p_{i}=1, the dataset is called pure.
The probability vector describing a given data set S with target y can be written as:

P_{y}=(\frac{|\sigma_{y=class_{1}}*S|}{|S|},…\frac{|\sigma_{y=class_{domain(y)}}*S|}{|S|})

To evaluate a split a_{i} regarding its goodness, the reduction in impurity of the target variable after the split a_{i} partitioning the set S in v branches (v_{i,j} \in dom(a_{i})) is measured:

\Delta \, \Phi(a_{i},S)=\Phi(P_{y}(S))-\sum_{j=1}^{|dom(a_{i})|} \, \frac{|\sigma_{a_{i}=v_{i}}*S|}{|S|}\,*\, \Phi(P_{y}(\sigma_{a_{i}=v_{i,j}}*S))

Information Gain based on Entropy

One of the most popular measures in the family of Impurity-based Criterions is Information Gain.
Information gain is usually calculated based on Entropy. Entropy can be seen as an impurity measure and the information gain is the splitting criterion. The concept originates from the field of information theory and can be defined as:

H_{k}(p_{i})=\sum_{i} \, p_{ki} \, * log_2 (\frac{1}{p_{ki}})=-\sum_{i} \, p_{ki} * log_2 (p_{ki})

where p_{ki} is the share of the i^{th} class of the target variable of the current (sub-) dataset on feature k.
So for a random set S=\{kid,kid,parent,kid,parent\}, the entropy is:

H(S)=-\frac{3}{5}*log_2 (\frac{3}{5})-\frac{2}{5}*log_2 (\frac{2}{5})=0.97

Depending on the number of distinct values k of the target variable y the maximum entropy is defined as log_2 (k). So for k=2 as in the case above, the maximum entropy is log_2 (2)=1.
This means that the function of the Entropy takes in our example for the data set S nearly its maximum – in other words the set is quite heterogenous regarding its values. The course of the entropy function in general is shown in figure 3.

Figure 3: Course of the different functions used for two-class node impurity measurements (cf Hastie et al (2017))

The information gain can be defined as the difference in entropy between two data sets S and A:

Gain(S,A)=H(S)-\sum_{v\in\,Values(A)} \frac{|S_{v}|}{|S|}\, * \, H(S_{v})

So in the context of decision trees, the information gain is the difference between the entropy of the set S at a given decision node and the average of the entropies of the distinct subdata sets which have been produced by a split of S. If the Information Gain is high, the respective split can be considered as being helpful in classifying the data in pure nodes. On the other hand, if the Information Gain is low, the respective split is not as efficient in splitting the data as possible pure nodes. So the information gain can be used to compare the different splits which are possible to perform at a given stage of the decision tree. Logically, when using Information Gain as Splitting Criterion, the inducer chooses the split with the highest information gain.

Gini Index

While the logic of Information Gain is built clearly on the concept of entropy, the Gini Index uses the divergences between the probability distributions of the target variable values. It can be defined as:

\begin{array}{lcl}Gini(y,S)=\,1-\sum_{c_{j}\,\epsilon\,dom(y)}\, (\frac{|\sigma_{y=c_{j}}*S|}{|S|}) \\\\Gini(y,S)=\,1-\sum_{i=1}^{c}\,(p_{i})^{2} \\\\Gini(y,S)=\,1-Impurity\,Function \end{array}

Given two classes c_{1} and c_{2} within the dependent variable y in a data set S with |S|=9 . For c_{1} , there is S_{1}=3 and the rest of the samples are classified being c_{2} , S_{1}=6 . Put this relation into the probabilistic form, it is possible to state for the two classes: \\ P_{1}=\frac{3}{3+6}=\frac{1}{3} and P_{2}=\frac{6}{3+6}=\frac{2}{3} . \\ So, to calculate the Gini-Index, the above values are just put in the given formula:

Gini(y,S)=1-({\frac{1}{3}}^{2}+{\frac{2}{3}}^{2})=\frac{4}{9}\approx\, 0.45

As the data set in the example is quite heterogenous for reasons of comparaison, the Gini-Index of a data set with P_{1}=\frac{1}{9} and P_{2}=\frac{8}{9} :

Gini(y,S)=1-({\frac{1}{9}}^{2}+{\frac{8}{9}}^{2})=\frac{16}{81}\approx\, 0.2

The Gini-Index for a more heterogenous data set is bigger than the latter one of a more homogenous data set. To choose which split should be chosen in a given situation, for every possible split, the Gini-Index is calculated. Then the split with the smallest Gini-Index is chosen, because it provides the most homogenous child nodes. The Gini-Index is a measure which favors in contrast to the information gain large partitions and less numerous outcomes.

Normalized impurity-based Criterion: Gain Ratio

A problem in using information gain to decide which attribute to split on is that the uncertainty measure tends naturally to drift to splits with numerous outcomes, because it favors fewer small partitions. Using the Information Gain G(S,A) is e.g. maximal if S_{i} contains only a single case. \\ To workaround this problem, Quinlan’s Gain Ratio applies with the so-called „`split info“‚ P(S,A) a kind of normalization of the Information gain. The split information indicates the potential information generated by dividing S into n subsets:

P(S,A)=-\sum_{i=1}^{t} \frac{|S_{i}|}{|S|} \, * \, log_2 (\frac{|S_{i}|}{|S|})

then the Gain Ratio can be calculated as:

Gain Ratio=\frac{G(S,A)}{P(S,A)}

As the formula shows quite obviously, the Gain Ratio is small, if the value in the denominator, the split information, takes on a high value. And the split information takes on higher values, if the data set concerned is broken down in numerous outcomes for a given split.

To choose the optimal split in a given situation, the split which exhibits the maximal Gain Ratio while the Split information measure is minimized is considered to be the optimal one.

Splitting Criterion for numerical features: \\ Within-nodes sum of squares

The above mentioned measures are usually used in situation, where the features are either categorical or discretized numerical features. The within-nodes sum of squares can in contrast output a decision criterion for numerical variables without prior discretization. The heterogenity of a given dataset is evaluated by the following formula:

i(\tau)=\sum \,(y_{i}-\bar{y}(\tau))^{2} 

As the formula points out, the Sum of squared Error (SSE) between each element of the response variable y_{i} of the respective, resulting node \tau of a potential split and the mean over all cases of this node is determined. The heterogenity of the split in question can then be measured by summing up all i(\tau) ’s of the respective split.

The split with the highest drop in within-nodes sum of squares compared to the value of the measure of the parent node is chosen.

Pruning

Trees tend to overfit the train data on which the tree has been trained on, because of their greedy and exhaustive nature. Pruning is a method within the tree building process to prevent this overfitting. \\ In the method, the pruning algorithm is cutting branches, just like a gardener, that aren’t beneficial to a good generalization capability of the tree. As a first crude separation, it is possible to distinguish pruning into two fields:

  • Pre-Pruning and
  • Post-Pruning

These concepts are described in the following part of the article.

Pre-Pruning

Pre-Pruning can be described in other words as early stopping the algorithm from further execution. Within the growing phase, the inducer checks if the predefined stopping criteria is fulfilled. If a branch does satisfy one of these criteria the further division of this part of the tree is instantly stopped and the algorithm proceeds with the next branch. \\ In that way, the tree procedure is stopped before the tree produces a structure too complex preventing the final model to generalize well on unseen data. Common stopping criteria could be for example:

  • A predefined tree depth has been reached.
  • The cross-validation error does not decrease significantly, when developping the branch in question.

Post-Pruning

In contrast to Pre-Pruning, in Post-Pruning, the inducer grows first of all a full grown tree which might be prone to overfit the underlying training data.  Then in the second step, the Post-Pruning algorithm cuts the respective subtrees considered to be harmful to the performance of the tree in question.

Error-based Pruning

As already mentioned, the post-pruning process tries to cut down branches of the tree which aren’t beneficial to its generalization performance on unseen data. The problem is to find a measure, that indicates which part of the tree can be pruned. A tree built on the integral training data set shows logically an increase in error rate ( \frac{misclassified\,samples\,of\,the\,node}{number\,of\,samples\,at\,node} ) while being pruned, because the tree was built to fit perfectly the training data structure. \\ So, some pruning methods don’t take the whole training set to built the tree, but split it before training into a training and a hold-out set. Then after having built the model based on the training set, for each node, the error rate is evaluated on the hold-out set and compared to the tree without the subtree in question. If the error rate is lower without the subtree, the latter is pruned. \\ But this is particularly in situations, where the training data is scarce quite problematic. Error-based pruning goes another statistically maybe a bit questionable way: \\ First of all, it uses all available training data to build the tree. Then it assumes that the given distribution at each respective leaf is just a subsample of the respective integral binomial, distributed population covered by this leaf. Due to the fact, that the probability of error cannot be determined exactly, the method tries to estimate it using its (posterior) probability distribution and its confidence level. It is possible to find the upper limit on the probability from the confidence level for the binomial distribution. So, the predicted error rate is just set equal with the upper limit of the binomial distribution (default: 25 %), following the reasoning that the tree model want to minimize the error rate. \\ Considering a leaf, if an event happens M times in N trials, the probability p can be estimated calculating \frac{M}{N} . To find the upper limit p_{r} such that p\,\leq\,p_{r} for a given confidence for a given confidence 1-CF , p_{r} is related as follows to CF :

  CF= \begin{cases}(1-p_{r})^{N} \qquad for\,\,M=0\\\ \\\sum_{i=0}^{M}\, {N\choose i}\,*{p_{r}}^{i}\,*\,(1-p_{r})^{N-1} \qquad for\,\,M>0\end{cases}

So, the general idea is, starting from the leaves, to measure with the method explained above the error rate for a given subtree and compare it to the error rate of the node above if the latter is replaced with the most common value. When the error rate of the leaves is higher than the error rate at the collapsed node, the subtree is pruned and the collapsed node is retained. \\
An example for the method could be helpful to understand the concept in more depth. Considering the part at node T2 of the tree (Example from Quinlan’s work) illustrated in figure 4, a given decision criterion has split up the current  dataset at this node of 15 Democrats and one Republican into three leaves. Now the question to answer is, if this split is beneficial in terms of error rate or if the leaves L3,L4 and L5 can be collapsed to build to form the leaf at node T2 predicting the most common value Democrats. 

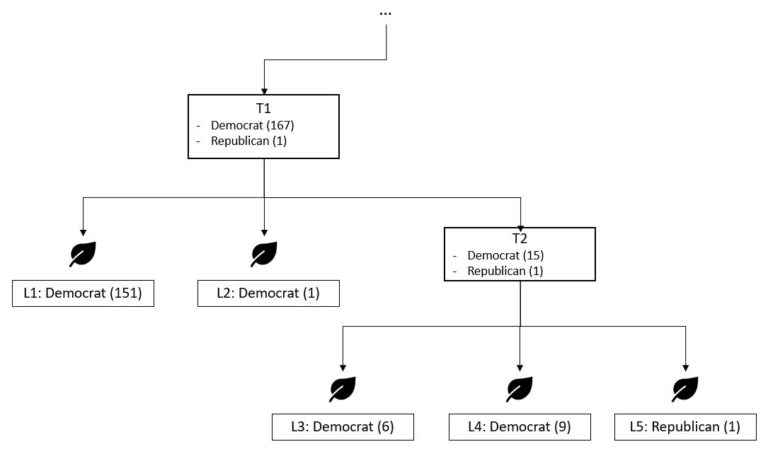
Figure 4: Example subtree to explain Error-based pruning (cf. Quinlan (1993))

As there aren’t any misclassification at L3 M=0 and N=6 . Therefore:

\begin{array}{lcl}CF=(1-p_{r})^{N} \\\\Gini(y,S)=\,1-\sum_{i=1}^{c}\,(p_{i})^{2} \\\\0.25=(1-p_{r})^{6} \\\\ p_{r}=1-\sqrt[6]{0.25}=0.206 \end{array}

For L4 there’s also no misclassificated observation M=0 and N=9 . Therefore:

p_{r}=1-\sqrt[9]{0.25}=0.143

and for L5, no misclassification can be observed ( M=0 ) and N=1 . Therefore:

p_{r}=1-\sqrt[1]{0.25}=0.75

For the number of predicted error for this subtree, this means:

6*0.206+9*0.143+1*0.75=3.273

The above predicted value should be compared to the hypothetical leaf, what can be produced in collapsing L3, L4 and L5. The predicted value of the resulting leaf T2 would be „`Democrat“‚, because it is the most frequent value at the leaf. In total, there are N=16  observations, but M=1  misclassification, because on value is „`Republican“‚. Therefore:

\begin{array}{lcl}0.25={16\choose 0}*p_{r}^{0}*(1-p_{r})^{16-0}+{16\choose 1}*p_{r}^{1}*(1-p_{r})^{16-1} \\\\0=(1-p_{r})^{16}+16*p_{r}*(1-p_{r})^{15}-0.25 \\\\ pr=0.1596 \end{array}

The above equation can be solved applying common method for the determination of zeros such as Newton or Regula Falsi Method. The number of predicted error for this hypothetical leaf T2 would be:

16*0.1596=2.5536

So the number of predicted errors of and the error rate for the leaf T2 is lower than the value of the subtree (predicted error=3.273) and therefore the subtree can be collapsed. \\ In the next step, it will be verified if the subtree beneath T1 can be collapsed and so on. In this manner, the algorithm proceeds bottom up until the tree gains its optimal structure.

Cost Complexity Pruning

Cost Complexity Pruning which is also known as „`weakest link pruning“‚ or „error complexity pruning“ is another popular approach to prevent a tree from overfitting within the post-pruning process. The idea behind the method is to generate series of differently pruned trees to determine for each of them the classification error on an independently hold-out data set. The pruned tree attaining the least error is then chosen to be the final model. \\ In general, within the pruning process, the Cost Complexity function needs to be optimized:

\begin{array}{lcl}R_{\alpha}(T)=R(T)+\alpha\,*\,|T| \\\\where: \qquad R(T)\coloneqq\,error\,rate\,at\,subtree\,T  \\\\\qquad \qquad \qquad \alpha\coloneqq\,complexity\,cost\,parameter  \\\\ \qquad \qquad \qquad |T| \coloneqq\,number\,of\,leaves\,of\,tree\,T \end{array}

To examine at which position it would be raisonable to prune the integral tree, the difference in terms of the cost function value between the tree T and its subtree ( T-T_{t}) is calculated:

\begin{array}{lcl}R_{\alpha}(T-T_{t})-R_{\alpha}(T)=R(T-T_{t})+\alpha \, * \, |T-T_{t}|-R(T)-\alpha \,* \, |T| \\\\ = \, R(T-T_{t}) + \alpha \, * \, (|T-T_{t}|-|T|)-R(T)  \\\\= R(T)-R(T_{t})+R(t)-R(T)+ \alpha * (|T|-|T_{t}|+1-|T|) \\\\ = R(t)-R(T_{t})+ \alpha * (1-|T_{t}|) \\\\ where:  t \coloneqq \, node \, t \\\\  \qquad T_{t} \coloneqq \, subtree \, T_{t} \, with \, root \, at \, t \end{array}

setting this difference to zero, in terms of \alpha , this would be:

\begin{array}{lcl} \alpha * (1-|T_{t}|)=R(T_{t})-R(t)  \\\\ \alpha = \frac{R(T_{t})-R(t)}{(1-|T_{t}|)}  \\\\ \alpha = \frac{R(t)-R(T_{t})}{(|T_{t}|-1)}  \end{array}

R(t)-R(T_{t}) is the reduction in error between node t and the subtree T_{t} and (T_{t}-1) gives out the number of leaves to prune. So \alpha can be understood being the reduction in error per leaf and can therefore be used to determine the value of the subtree. \\ So, if the value of \alpha is high, the value of the predictional capabilities of the subtree is high and if \alpha is low, the subtree doesn’t lead to much more insight as the tree without the subtree in question. \\ The pruning algorithm can be subsumed as follows:

Algorithm 2: Algorithm applied for Cost Complexity Pruning

The goal is to find the tree that performs best on unknown data. So, the pruned trees T_{1},…,T_{k} corresponding to the \alpha ’s, determined in the last step, are then tested on the hold-out set and the tree that performs best in terms of misclassification rate is chosen to be the final tree. \\ If data is scarce and it is complicated to separate the data into a training and a hold-out set, it is possible to proceed with this approach using crossvalidation and using in this way the whole training set. \\ As already illustrated in the last pruning method, an example could shed a bit more light in the concept:

Assuming the tree T in figure 5. \\ So, for the first iteration, the \alpha ’s for t_{0} , t_{1} and t_{3} are calculated. In the calculation, r(t) can be understood as the misclassification error at the respective node and p(t) as the proportion of data items which reached node t .

\begin{array}{lcl} t_{0}: \, R(t)=r(t)*p(t)=\frac{12}{24} * \frac{24}{24}=\frac{12}{24} \\\\  R(T_{t})=0 \, , \, because \, the \, full \, grown \break \, tree \, classifies \, everything \, exact \\\\  |T|=4 \\\\  \alpha_{t_{0}}=\frac{R(t)-R(T_{t})}{|T_{t}-1|}=\frac{\frac{12}{24}-0}{4-1}=0.16 \end{array}

and

\begin{array}{lcl}  t_{1}: \, R(t)=r(t)*p(t)=\frac{4}{16} * \frac{16}{24}=\frac{4}{24} \\\\ R(T_{t})=0 \, , \, because \, the \, full \, grown \, tree \, classifies \, everything \, exact  \\\\  |T|=3  \\\\ \alpha_{t_{1}}=\frac{R(t)-R(T_{t})}{|T_{t}-1|}=\frac{\frac{4}{24}-0}{3-1}=0.083  \end{array}
Figure 5: Example tree to explain Cost Complexity Pruning
\begin{array}{lcl} t_{3}: \, R(t)=r(t)*p(t)=\frac{2}{6} * \frac{6}{24}=\frac{1}{12} \\\\  R(T_{t})=0 \, , \, because \, the \, full \, grown \, tree \, classifies \, everything \, exact  \\\\  |T|=2 \\\\ \alpha_{t_{3}}=\frac{R(t)-R(T_{t})}{|T_{t}-1|}=\frac{\frac{1}{12}-0}{2-1}=0.083 \end{array}

So, in this example in the first iteration step, the tree would be pruned at t_{3} , because of its low \alpha value and (opposed to pruning at t_{1} )  the lowest number of leaves. The tree is subsequently collapsed at t_{3} and this new tree is then used in the next iteration step to find out the next pruning candidat. The method stops when only t_{0} , the stump, is left.

ID3 and C4.5

The ID3 as well as the C4.5 are two of the most popular decision tree inducer in data science. ID3, the iterative Dichotomizer, and the C4.5 are insofar related that the ID3 is the immediate predecessor of C4.5. The origins of the inducers can be traced back to research on tree learners in the late ’50’s and work on ID3 was published first by Quinlan (1979). The further development and improvement of the inducer, namely C4.5 and later C5.0, appeared in the ’90’s.

ID3

The ID3 inducer is one of the first more popular ones and is quite simple in its structure (600 lines of pascal). In general, it follows the divide-and-conquer procedure described at the beginning of the section „`Underlying Math“‚. \\ In top-down greedy approach, for each node the split maximizing the Information Gain is chosen. The algorithm creates favorably multiway splits and exhibits therefore usually wide structures. When all training samples are correctly classified into homogenous leaves, the ID3 stops further execution.  The inducer tries to produce short trees with an understandable and simple structure what can be seen as its biggest virtue. Concerning the possible data types, the ID3 is only able to handle categorical data. To search for the optimal tree, ID3 makes use of the entire hypothesis space, but does not guarantee an optimal solution, because the algorithm tends to produce trees which got stuck in local optima. In addition to that, the inducer does not provide any algorithm to prune the tree, so the produced tree is prone to overfit. Further limitations of the ID3 include for example that continuous scaled data has to be converted into bins before it is possible to use the data to induce a tree. In contrast to C4.5 and CART, the ID3 lacks in addition to that a strategy to handle missing data. 

C4.5

As seen in the last section, the ID3 inducer comprises a simplistic possibility to build a rule based tree classifier based on the underlying data. But there are also some limitations when using the ID3. The C4.5, firstly published by Quinlan(1993), tries to handle the mentioned drawbacks and can be understood as an evolution of the ID3 inducer. Using the Divide-and-Conquer building approach, the inducer provides the following improvements:

  • Beside the possibility to apply pre-pruning methods, the inducer implements Error-based pruning to tackle the problem of overfitting, which isn’t implemented in ID3.
  • Concerning the handling of missing data, ID3 does not provide a way to handle this kind of values. In contrast, C4.5 is able to handle the missing data using a form of corrected gain ratio.
  • Opposed to ID3, C4.5 does not only handle nominal attributes, but is also able to handle continuous features. For handling nominal features, the inducer proceeds as in the ID3, but uses the Gain Ratio as splitting criterion to find the best feature to split on. Dealing with continuous variables, the values of the attribute of the data set in question are first of all arranged in ascending order \{v_{1},v_{2},…,v_{m}\} . Then any threshold between  v_{i} and v_{i+1} is considered and for each interval the midpoint \frac{v_{i}+v_{i+1}}{2} is calculated. C4.5 takes then always the largest value that does not exceed the respective midpoint. Then after having calculated and examined these m-1 thresholds, the threshold \theta is retained that maximizes the gain ratio

Due to its splitting criterion, the gain ratio, in contract to the pure information gain used by ID3, C4.5 splits the data in favor of splits with less numerous outcome, what makes it less complex and prone to overfitting. \\ Quinlan’s latest release version of the inducer under a payed licence is the C5.0. In addition to the improvements to ID3 already mentioned, this algorithm uses less memory, builds smaller rule sets and is more accurate than C4.5.

CART

In their book „`CART: Classification and Regression Trees“‚, Breiman et al (1984) presented the CART tree inducer. \\ CART uses as the ID3 and the C4.5, the divide-and-conquer method to grow the classification or regression tree. But there are also some differences to observe:

One major difference between CART and C4.5 is the tree structure. CART splits the data set always in binary partition, so that there are always two outgoing edges from a node. \\ For classification trees, the inducer uses not the Gain Ratio or the Information Gain, but the Gini Index to measure the heterogenity of the data set.  The measure is then calculated for each of the distinct values for the respective p attributes, e.g. asking for a data set S=\{red,red,green,blue\} „`is the color red?“‚ classifying the data into „`yes“‚ or „`no“‚. Then the optimal feature in terms of capability to produce homogenous subsets is chosen as the splitting point. \\ For regression trees, the inducer strives to find the optimal splitting point s which minimizes the within-nodes sum of squares: \\\\ \begin{array}{lcl} \\\\  \sum_{x_{i} \epsilon R_{1}(j,s)} \, (y_{i}-\hat{y}_{R_{1}})^{2} \, + \, \sum_{x_{i} \epsilon R_{2}(j,s)} \, (y_{i}-\hat{y}_{R_{2}})^{2} \\\\ where: \qquad R_{1}(j,s)=\{X|X_{j}<s\} \,\,\, and \,\,\, R_{2}(j,s)=\{X|X_{j} \geq s\} \\\\ \end{array}

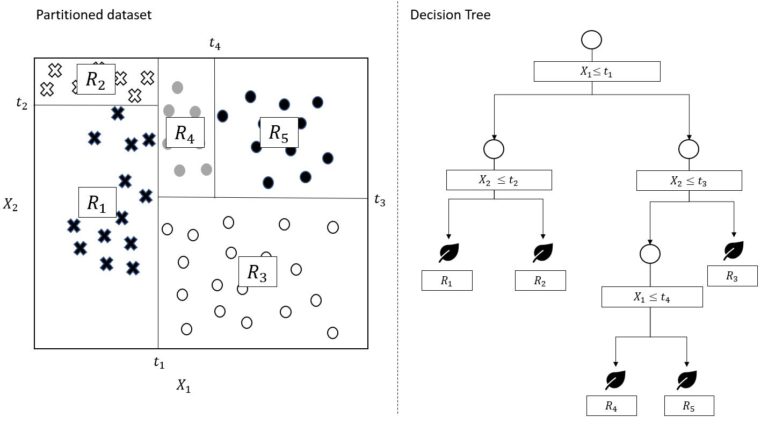
Figure 6: Graphical representation of a Regression Tree

So, for every distinct value on the p attributes the within-nodes sum of squares is calculated. Then the split with the minimum value of this measure is chosen to split the data in two regions. This process is then repeated recursively until the partitions are homogenous enough.

In figure 6, a decision tree has been grown and on the right side, the model is shown in the tree structured fashion already explained in the preceding sections of the article. On the left side, the same tree breaks down the data in a two dimensional space. For example, at splitting point t_{1} , the data is separated into the data satisfying the test X_{1} > t_{1} and the data satisfying X_{1} \leq t_{1} . Then following the left branch ( X_{1} \leq t_{1}), the data subset is split up into R_{1} ( X_{2}\leq T_{2}) and R_{2} ( X_{2} > T_{2} ). For region 1, R_{1} , the predicted value for unknown data
would consist of the average of all data satisfying the rule set of R_{1} out of the training set. The same applies to all other regions.

Another difference lies in the pruning method used to prevent overfitting. In contrast to C4.5, which uses error-based pruning, cost-complexity pruning, which was already explained in the preceding sections, is applied.

Concerning missing values, CART shows a specific manner to deal with this kind of data. It uses so-called Surrogate splits. In fact, the inducer doesn’t only searches for the best split in terms of the splitting criterion, but also the second best, the surrogate split. If the unknown data, which the tree has to predict is for some reason missing on the primary split, the surrogate is used.

One of the biggest virtue of CART can be at the same time also a controversial vice. The CART inducer uses binary splits, what makes the tree quite simple and prevents the inducer from growing wide trees with numerous outcomes. But on the other hand, it happens that CART uses binary splits on the same attribute on different levels, what makes it more difficult for the user to interpret the model. In this case, the possibility to interpret the tree might seem to be hindered, but on the other hand in this way, complex relationships in the data could be uncovered, leading to better results. \\ To finish the section about CART, it is worth mention that this inducer is the most used in the current data science libraries such as python because of its virtues to grow decision trees. But in general, over time the approaches developed by Quinlan(ID3, C4.5 and the C5.0) became more and more similar to CART and some software also uses C4.5 to tackle data science problems by tree models.

Implementation of a simple decision tree in Python

Advantages and limitations of decision trees​

One have to distinguish between the virtues and limitations of decision trees opposed to other machine learning algorithms and the advantages and limitations of the respective tree inducer in relation to other tree inducer. The latter have already been illustrated in the respective section for the ID3, the C4.5 and the CART inducer. \\
The virtues and limitations of decision tree as to other Machine Learning Algorithms are described in the following:

Advantages of decision trees

First of all, decision trees are compared to other Machine Learning models thanks to its simple structure easy to interpret. In addition to that, for other models there is a need to prepare the data before using the model, because most models can’t deal with noisy and/or missing data. Modern tree models do have the intrinsic ability to deal with this kind of data property without any need for upfront preparation. Beside the fact, that modern tree inducers accept both numeric and categorical attributes to grow a tree. Tree models are in contrast to other linear classifier also able to model a high degree of non-linear relationships in the underlying data. When the model is properly trained and possible overfitting treated, the model is also known to be robust to errors.

Limitations of decision trees

But tree models exhibit beside their numerous virtues, also some limitations, which will be the subject of discussion in this part of the article. \\
Tree models in general tend to overfit, if the tree is too complex. To tackle this problem, modern tree models can be tuned by changing several hyperparameters such as minimal node size, the choice of the splitting criterion or the maximum depth of the tree. In addition to that, it is possible to implement pruning method as already mentioned to assure a good generalization capability. \\  
Beside the problem of overfitting, trees show also high variance. Small changes in input data can lead to a different sequence of splits induced and so the tree structure can be very different for the same data set. To fight this weakness of tree learners, ensembling methods such as random forest or boosting method can be applied, where more than one tree model is combinated to come to a competitive, robust overall result. \\  

Sources

  • Garcia, Salvador; Luengo, Julian; Herrera, Francisco; García, Salvador; Luengo, Julián (2015): Data Preprocessing In Data Mining. Cham, Heidelberg, New York, Dordrecht, London: Springer Vieweg; Springer (Intelligent systems reference library, Volume 72).
  • Gupta, Shubham: Decision Tree. Online verfügbar unter https://www.hackerearth.com/fr/practice/machine-learning/machine-learning-algorithms/ml-decision-tree/tutorial/.
  • Hastie, Trevor; Tibshirani, Robert; Friedman, Jerome H. (2017): The elements of statistical learning. Data mining, inference, and prediction. Second edition, corrected at 12th printing 2017. New York, NY: Springer (Springer series in statistics).
  • Hoare, Jake (na): Machine Learning: Pruning Decision Trees. Hg. v. Displayr Blog. Online verfügbar unter https://www.displayr.com/machine-learning-pruning-decision-trees/?utm_referrer=https%3A%2F%2Fwww.google.com%2F.
  • Jazuli, Hafidz: An Introduction to Decision Tree Learning: ID3 Algorithm. Hg. v. medium.com. Online verfügbar unter https://medium.com/machine-learning-guy/an-introduction-to-decision-tree-learning-id3-algorithm-54c74eb2ad55.
  • Kohavi, Ron; Quinlan, Ross (1999): Decision Tree Discovery. Stanford University, Stanford.
  • Marsland, Stephen (2015): Machine learning. An algorithmic perspective. Second edition. Boca Raton, FL: CRC Press (Chapman & Hall / CRC machine learning & pattern recognition series).
  • Mingers, John: An Empirical Comparison of Pruning Methods for Decision Tree Induction. In: Machine Learning, Bd. 4, S. 227–243.
  • Mitchell, Tom M. (2010): Machine learning. International ed. New York, NY: McGraw-Hill (McGraw-Hill series in computer science).
  • Nisbet, Robert; Miner, Gary; Yale, Ken; Elder, John F.; Peterson, Andy (2018): Handbook of statistical analysis and data mining applications. 2nd edition. London, San Diego: Academic Press an imprint of Elsevier.
  • Prune (2018): hypothesis function space in decision tree. Hg. v. stackoverflow.com. Online verfügbar unter https://stackoverflow.com/questions/51266841/hypothesis-function-space-in-decision-tree.
  • Quinlan, J. R. (1986): Induction of Decision Trees. In: Machine Learning 1 (1), S. 81–106.
  • Quinlan, John Ross (1993): C4.5. Programs for machine learning. San Mateo, Calif: Morgan Kaufmann Publishers (The Morgan Kaufmann series in machine learning). Online verfügbar unter http://search.ebscohost.com/login.aspx?direct=true&scope=site&db=nlebk&db=nlabk&AN=919367.
  • Rokach, Lior; Maimon, Oded (2015): Data mining with decision trees. Theory and applications. Second edition. Hackensack New Jersey: World Scientific.
  • Russell, Stuart J.; Norvig, Peter (2016): Artificial intelligence. A modern approach. Unter Mitarbeit von Ernest Davis und Douglas Edwards. Third edition, Global edition. Boston, Columbus, Indianapolis: Pearson (Always learning).
  • scikit-learn.org (na): 1.10. Decision Trees. Hg. v. scikit-learn.org. Online verfügbar unter https://scikit-learn.org/stable/modules/tree.html#tree-algorithms-id3-c4-5-c5-0-and-cart.
  • Singh, Sonia; Gupta, Priyanka (2014): Comparative Study ID3, CART and C4.5 Decision Tree Algorithm: A Survey. In: International Journal of Advanced Information Science and Technology (IJAIST) 27 (27), S. 97–103.
  • Wu, Xindong; Kumar, Vipin; Ross Quinlan, J.; Ghosh, Joydeep; Yang, Qiang; Motoda, Hiroshi et al. (2008): Top 10 algorithms in data mining. In: Knowl Inf Syst 14 (1), S. 1–37. DOI: 10.1007/s10115-007-0114-2.
  • Yohannes, Yisehac; Webb, Patrick (1999): Classification and regression trees, CART. A user manual for identifying indicators of vulnerability to famine and chronic food insecurity. Washington D.C.: International Food Policy Research Institute (Microcomputers in policy research, 3).

Author: Robin Wesselmann

Schreibe einen Kommentar

Deine E-Mail-Adresse wird nicht veröffentlicht. Erforderliche Felder sind mit * markiert